利用平行四边形的性质证明角相等、边相等和直线平行
如图,已知E,F分别是ABCD的边CD,AB上的点,且DE=BF.求证:AE∥CF.
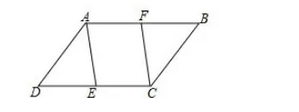
分析:由四边形ABCD为平行四边形可得:AB=CD,AB∥CD。由已知条件DE=BF,根据等边减等边可得AF=CE,由此可证明四边形AECF为平行四边形,从而得到AE∥CF。通过此题可知,平行四边形又为我们证明直线平行增加了一种方法。
证明:∵四边形ABCD为平行四边形,∴AB∥CD,AB=CD
又∵DE=BF,∴AB-BF=CD-DE,即AF=CE
∴四边形AECF为平行四边形,∴AE∥CF
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
