数列{an}的各项均为正数,Sn为其前n项和,对于任意n∈N*,总有an , Sn , an2成等差数列.
(1)求数列{an}的通项公式;
(2)设 , 数列{bn}的前n项和为Tn , 求证:
, 数列{bn}的前n项和为Tn , 求证: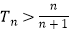 .
.
解:(1)由已知:对于n∈N* , 总有2Sn=an+an2①成立
∴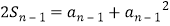 (n≥2)②
(n≥2)②
①﹣②得2an=an+an2﹣an﹣1﹣an﹣12 , ∴an+an﹣1=(an+an﹣1)(an﹣an﹣1)
∵an , an﹣1均为正数,∴an﹣an﹣1=1(n≥2)∴数列{an}是公差为1的等差数列
又n=1时,2S1=a1+a12 , 解得a1=1,∴an=n.(n∈N*)
(2)解:由(1)可知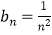 ∵
∵ =
=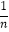 -
-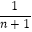
∴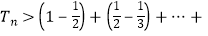 (
(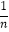 -
-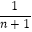 )=
)=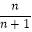
(1)根据an=Sn﹣Sn﹣1 , 整理得an﹣an﹣1=1(n≥2)进而可判断出数列{an}是公差为1的等差数列,根据等差数列的通项公式求得答案.
(2)由(1)知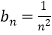 , 因为
, 因为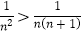 =
=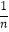 -
-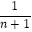 , 所以
, 所以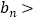
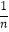 -
-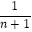 , 从而得证.
, 从而得证.
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
