二次函数y=ax2+bx+4的图象与x轴交于两点A、B，与y轴交于点C，且A（﹣1，0）、B（4，0）．

二次函数y=ax2+bx+4的图象与x轴交于两点A、B，与y轴交于点C，且A（﹣1，0）、B（4，0）．

（1）求此二次函数的表达式；

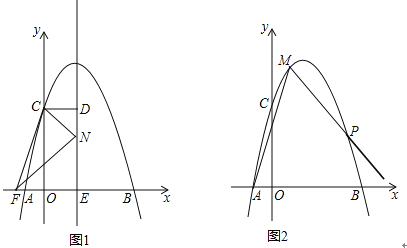
（2）如图1，抛物线的对称轴m与x轴交于点E，CD⊥m，垂足为D，点F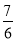（﹣，0），动点N在线段DE上运动，连接CF、CN、FN，若以点C、D、N为顶点的三角形与△FEN相似，求点N的坐标；

（3）如图2，点M在抛物线上，且点M的横坐标是1，将射线MA绕点M逆时针旋转45°，交抛物线于点P，求点P的坐标．

【答案】

（1）抛物线的解析式为y=﹣x2+3x+4；（2）点N的坐标为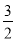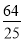（，）或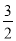（，2）；（3）P的坐标为（4，0）

【解析】

分析:（1）先求得点C的坐标，设抛物线的解析式为y＝a（x＋1）（x−4），将点C的坐标代入求得a的值，从而得到抛物线的解析式；

（2）先求得抛物线的对称轴，然后求得CD，EF的长，设点N的坐标为（0，a）则ND＝4−a，NE＝a，然后依据相似三角形的性质列出关于a的方程，然后可求得a的值；

（3）过点A作AD∥y轴，过点M作DM∥x轴，交点为D，过点A作AE⊥AM，取AE＝AM，作EF⊥x轴，垂足为F，连结EM交抛物线与点P．则△AME为等腰直角三角形，然后再求得点M的坐标，从而可得到MD＝2，AD＝6，然后证明∴△ADM≌△AFE，于是可得到点E的坐标，然后求得EM的解析式为y＝−2x＋8，最后求得直线EM与抛物线的交点坐标即可．

详解:

（1）当x=0时，y=4，∴C（0，4）．

设抛物线的解析式为y=a（x+1）（x﹣4），将点C的坐标代入得：﹣4a=4，解得a=﹣1，

∴抛物线的解析式为y=﹣x2+3x+4．

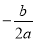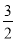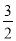（2）x==．∴CD=，EF=．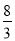

设点N的坐标为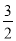（，a）则ND=4﹣a，NE=a．

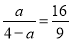当△CDN∽△FEN时，，即，解得a=，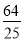

∴点N的坐标为（，）．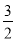

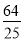当△CDN∽△NEF时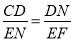，，即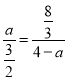，解得：a=2．

∴点N的坐标为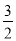（，2）．

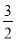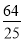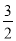综上所述，点N的坐标为（，）或（，2）．

（3）如图所示：过点A作AD∥y轴，过点M作DM∥x轴，交点为D，过点A作AE⊥AM，取AE=AM，作EF⊥x轴，垂足为F，连结EM交抛物线与点P．

∵AM=AE，∠MAE=90°， ∴∠AMP=45°．

将x=1代入抛物线的解析式得：y=6， ∴点M的坐标为（1，6）． ∴MD=2，AD=6．

∵∠DAM+∠MAF=90°，∠MAF+∠FAE=90°， ∴∠DAM=∠FAE．

在△ADM和△AFE中，，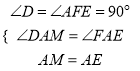

∴△ADM≌△AFE．

∴EF=DM=2，AF=AD=6．

∴E（5，﹣2）．

设EM的解析式为y=kx+b．

将点M和点E的坐标代入得：，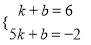

解得k=﹣2，b=8，

∴直线EM的解析式为y=﹣2x+8．

将y=﹣2x+8与y=﹣x2+3x+4联立，解得：x=1或x=4．

将x=4代入y=﹣2x+8得：y=0．∴点P的坐标为（4，0）．

点睛: 本题主要考查的是二次函数的综合应用，解答本题主要应用了待定系数法求一次函数、二次函数的解析式，相似三角形的性质、等腰直角三角形的性质、全等三角形的性质，通过作辅助线构造等腰直角三角形、全等三角形求得点E的坐标是解题的关键．