若点A（a，b）（其中a≠b）在矩阵M=<img alt="1" src="/tk/20210512/1620750862530.png"/> 对应

若点A（a，b）（其中a≠b）在矩阵M=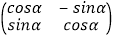 对应变换的作用下得到的点为B（﹣b，a），

（Ⅰ）求矩阵M的逆矩阵；

（Ⅱ）求曲线C：x2+y2=1在矩阵N=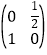所对应变换的作用下得到的新的曲线C′的方程．

【答案】

解：（Ι）∵点A（a，b）（其中a≠b）在矩阵M=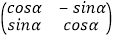 对应变换的作用下得到的点为B（﹣b，a），

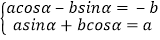∴得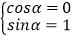

即M=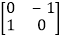，由M﹣1M=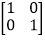得M﹣1=．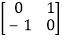

（Ⅱ）设P（x0 ， y0）是曲线C：x2+y2=1上任意一点，

则点P（x0 ， y0）在矩阵M对应的变换下变为点P′（x，y）

则有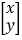=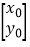，即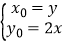

又∵点P在曲线C：x2+y2=1上，

∴4x2+y2=1，即曲线C'的方程为椭圆4x2+y2=1．

【解析】

（Ⅰ）根据二阶矩阵与平面列向量的乘法，确定矩阵M，再求矩阵的逆矩阵；

（Ⅱ）设曲线C上任意一点P（x0 ， y0），根据矩阵变换的公式求出对应的点P′（x，y），解出由x、y表示x0 ， y0的式子，将点P的坐标代入曲线C方程，化简即得曲线C'的方程．