如图所示，一质量为m=1kg的小球从A点沿光滑斜面轨道由静止滑下，不计通过B点时的能量损失，然后依次滑入两个相同的圆形轨道内侧，其轨道半径R=10cm，小球恰能通过第二个圆形轨道的最高点，小球离开圆形

如图所示，一质量为m=1kg的小球从A点沿光滑斜面轨道由静止滑下，不计通过B点时的能量损失，然后依次滑入两个相同的圆形轨道内侧，其轨道半径R=10cm，小球恰能通过第二个圆形轨道的最高点，小球离开圆形轨道后可继续向E点运动，E点右侧有一壕沟，E、F两点的竖直高度d=0.8m，水平距离x=1.2m，水平轨道CD长为L1=1m，DE长为L2=3m。轨道除CD和DE部分粗糙外，其余均光滑，小球与CD和DE间的动摩擦因数μ=0.2，重力加速度g=10m/s2。求：

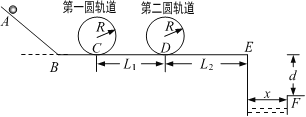
⑴小球通过第二个圆形轨道的最高点时的速度；

⑵小球通过第一个圆轨道最高点时对轨道的压力；

⑶若小球既能通过圆形轨道的最高点，又不掉进壕沟，求小球从A点释放时的高度的范围是多少？

【答案】

⑴1m/s⑵40N⑶0.45m≤h≤0.8m或h≥1.25m

【解析】

⑴小球恰能通过第二个圆形轨道最高点，有：

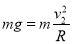
求得：υ2=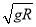=1m/s ①

⑵在小球从第一轨道最高点运动到第二圆轨道最高点过程中，应用动能定理有：

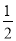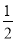−μmgL1=mv22−mv12 ②

求得：υ1=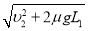=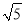m/s

在最高点时，合力提供向心力，即FN+mg=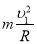 ③

求得：FN = m(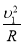−g)= 40N

根据牛顿第三定律知，小球对轨道的压力为：FN′=FN=40N ④

⑵若小球恰好通过第二轨道最高点，小球从斜面上释放的高度为h1，在这一过程中应用动能定理有：mgh1 −μmgL1 −mg 2R = 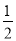mv22 ⑤

求得：h1=2R+μL1+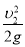=0.45m

若小球恰好能运动到E点，小球从斜面上释放的高度为h1，在这一过程中应用动能定理有：

mgh2−μmg(L1+L2)=0−0 ⑥

求得： h2=μ(L1+L2)=0.8m

使小球停在BC段，应有h1≤h≤h2，即：0.45m≤h≤0.8m

若小球能通过E点，并恰好越过壕沟时，则有

d =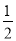gt2 →t =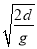= 0.4s ⑦

x=vEt →υE=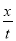=3m/s ⑧

设小球释放高度为h3，从释放到运动E点过程中应用动能定理有：

mgh3 −μmg(L1+L2)=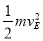−0 ⑨

求得：h3=μ(L1+L2)+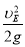=1.25m

即小球要越过壕沟释放的高度应满足：h≥1.25m

综上可知，释放小球的高度应满足：0.45m≤h≤0.8m或 h≥1.25m ⑩