如图所示，在三棱柱ABC—A1B1C1中，AA1⊥BC，∠A1AC＝60°，A1A＝AC＝BC＝1，A1B＝<img alt="1" src="/tk/202105

如图所示，在三棱柱ABC—A1B1C1中，AA1⊥BC，∠A1AC＝60°，A1A＝AC＝BC＝1，A1B＝.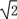

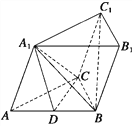
(1)求证：平面A1BC⊥平面ACC1A1；

(2)如果D为AB中点，求证：BC1∥平面A1CD.

【答案】

(1)详见解析;(2)详见解析.

【解析】

(1)先利用等边三角形和勾股定理得到线线垂直，再利用线面垂直的判定定理、面面垂直的判定定理进行证明;(2)先利用平行四边形和三角形的中位线证得线线平行，再利用线面平行的判定定理进行证明.

(1)因为∠A1AC＝60°，A1A＝AC＝1，

所以△A1AC为等边三角形.所以A1C＝1.

因为BC＝1，A1B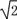＝，所以A1C2＋BC2＝A1B2.

所以∠A1CB＝90°，即A1C⊥BC.

因为BC⊥A1A，BC⊥A1C，AA1∩A1C＝A1，

所以BC⊥平面ACC1A1.

因为BC⊂平面A1BC，所以平面A1BC⊥平面ACC1A1.

(2)连接AC1交A1C于点O，连接OD.

因为ACC1A1为平行四边形，

所以O为AC1的中点.因为D为AB的中点，所以OD∥BC1.

因为OD⊂平面A1CD，BC1⊄平面A1CD，所以BC1∥平面A1CD.