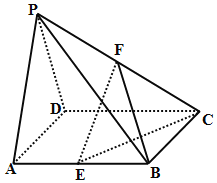
如图所示,在四棱锥P-ABCD中,底面ABCD是棱长为2的正方形,侧面PAD为正三角形,且面PAD⊥面ABCD,E、F分别为棱AB、PC的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD是棱长为2的正方形,侧面PAD为正三角形,且面PAD⊥面ABCD,E、F分别为棱AB、PC的中点.
(1)求证:EF∥平面PAD;
(2)求三棱锥B-EFC的体积;
(3)求二面角P-EC-D的正切值.
(1)见解析(2)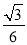 (3)
(3)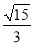
(1)取PD中点G,利用平几知识可得EFGA是平行四边形,即得EF∥AG,再根据线面平行判定定理得结论,(2)求体积关键在求高:取AD中点O,由面面垂直性质定理可得PO⊥面ABCD,即得高为PO一半,再代入锥体体积公式得体积,(3)求二面角关键在作出二面角的平面角,连OB交CE于M,由平几知识可得OM⊥EC.再利用三垂线定理可得PM⊥EC,即得∠PMO是二面角P-EC-D的平面角,最后再直角三角形中求∠PMO的正切值即可.
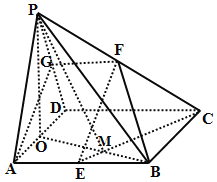
(1)证明:取PD中点G,连结GF、AG,
∵GF为△PDC的中位线,∴GF∥CD且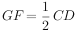 ,
,
又AE∥CD且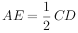 ,∴GF∥AE且GF=AE,
,∴GF∥AE且GF=AE,
∴EFGA是平行四边形,则EF∥AG,
又EF⊄面PAD,AG⊂面PAD,
∴EF∥面PAD;
(2)解:取AD中点O,连结PO,
∵面PAD⊥面ABCD,△PAD为正三角形,∴PO⊥面ABCD,且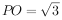 ,
,
又PC为面ABCD斜线,F为PC中点,∴F到面ABCD距离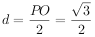 ,
,
故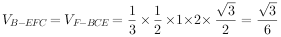 ;
;
(3)解:连OB交CE于M,可得Rt△EBC≌Rt△OAB,
∴∠MEB=∠AOB,则∠MEB+∠MBE=90°,即OM⊥EC.
连PM,又由(2)知PO⊥EC,可得EC⊥平面POM,则PM⊥EC,
即∠PMO是二面角P-EC-D的平面角,
在Rt△EBC中,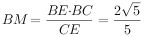 ,∴
,∴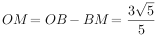 ,
,
∴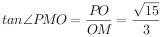 ,即二面角P-EC-D的正切值为
,即二面角P-EC-D的正切值为 .
.
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
