如图,在矩形ABCD中,AB=9,BC=6,若矩形AEFG与矩形ABCD是位似图形且相似比为<img alt="1" src="/tk/20210512/16207
如图,在矩形ABCD中,AB=9,BC=6,若矩形AEFG与矩形ABCD是位似图形且相似比为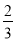 ,求C,F之间的距离.
,求C,F之间的距离.
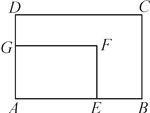
C,F之间的距离为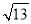
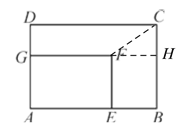
如图,过点F作FH⊥BC于点H,连接CF,由已知容易求得EF=4,AE=6,从而可得CH=BC-BH=BC-EF=2,FH=BE=AB-AE=3,这样在Rt△CHF中,由勾股定理即可求得CF=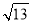 .
.
如图,过点F作FH⊥BC于点H,连接CF,
∴∠BHF=∠CFH=90°,
∵矩形AEFG与矩形ABCD是位似图形且相似比为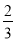 ,AB=9,BC=6,
,AB=9,BC=6,
∴∠B=∠BEF=90°,AE=6,EF=4,
∴四边形BEFH是矩形,
∴BH=EF=4,FH=BE=AB-AE=3,
∴CH=BC-BH=6-4=2,
∴在Rt△CFH中,CF=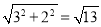 ,即点C和点F之间的距离为
,即点C和点F之间的距离为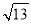 .
.
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
