设函数<img alt="1" src="/tk/20210512/1620761644966.png"/>为定义在R上的奇函数，对任意<im
设函数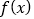
为定义在R上的奇函数，对任意
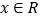都有
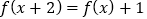成立，则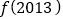
的值为（ ）
A.1006
B.1007
C.1006.5
D.无法确定
【答案】C
【解析】因为，函数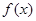
为定义在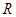
上的奇函数，对任意
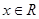都有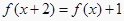
成立，所以，
， 
， 
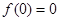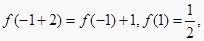
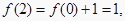
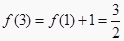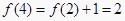， ……由此归纳出
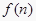构成公差为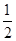
的等差数列，所以，
=
=
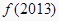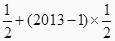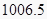， 故选C。
【考点精析】认真审题，首先需要了解函数奇偶性的性质(在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇)，还要掌握等差数列的通项公式（及其变式）(通项公式：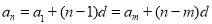
或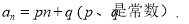
)的相关知识才是答题的关键．
版权声明
声明：有的资源均来自网络转载，版权归原作者所有，如有侵犯到您的权益
请联系本站我们将配合处理！