已知函数f(x)=<img alt="1" src="/tk/20210512/1620762019597.png"/>.
已知函数f(x)=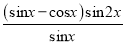 .
.
(1)求f(x)的定义域及最小正周期;
(2)求f(x)的单调递增区间.
【答案】(1) 详见解析;(2) [kπ-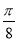 ,kπ)∪(kπ,kπ+
,kπ)∪(kπ,kπ+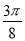 ]k∈Z.
]k∈Z.
试题分析:(1)根据正弦函数的性质求出函数的定义域,再根据二倍角公式和两角和与差的正弦公式化简,得到函数的最小正周期;(2)由正弦函数的单调区间求解即可.
试题解析:
(1)由sinx≠0得x≠kπ(k∈Z),故f(x)的定义域为{x|x∈R且x≠kπ,k∈Z}.
∴f(x)=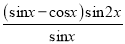
=2cosx(sinx-cosx)=sin2x-cos2x-1
=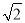 sin(2x-
sin(2x-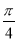 )-1,∴f(x)的最小正周期T=
)-1,∴f(x)的最小正周期T=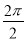 =π.
=π.
(2)函数y=sinx的单调递增区间为[2kπ-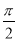 ,2kπ+
,2kπ+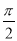 ](k∈Z).
](k∈Z).
由2kπ-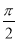 ≤2x-
≤2x-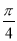 ≤2kπ+
≤2kπ+ ,x≠kπ(k∈Z),
,x≠kπ(k∈Z),
得kπ-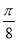 ≤x≤kπ+
≤x≤kπ+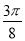 ,x≠kπ(k∈Z).
,x≠kπ(k∈Z).
∴f(x)的单调递增区间为[kπ-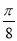 ,kπ)∪(kπ,kπ+
,kπ)∪(kπ,kπ+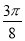 ]k∈Z.
]k∈Z.
点睛:本题考查三角函数的图象与性质,以及同角三角函数的基本关系,属于中档题目.三角函数的化简往往利用诱导公式,两角和与差的公式以及二倍角公式化为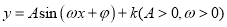 函数形式,再根据正弦函数的有界性,单调区间,周期性和对称性等求解.
函数形式,再根据正弦函数的有界性,单调区间,周期性和对称性等求解.
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
