袋子中放有大小和形状相同的小球若干个,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个.已知从袋子中随机抽取1个小球,取到标号是2的小球的概率是<img alt="1&q
袋子中放有大小和形状相同的小球若干个,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个.已知从袋子中随机抽取1个小球,取到标号是2的小球的概率是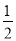 .
.
(1)求n的值;
(2)从袋子中不放回地随机抽取2个小球,记第一次取出的小球标号为a,第二次取出的小球标号为b.
①记事件A表示“a+b=2”,求事件A的概率;
②在区间[0,2]内任取2个实数x,y,求事件“x2+y2>(a-b)2恒成立”的概率.
【答案】(1)2;(2)①.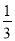 ;②.
;②.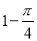 .
.
(1)根据从袋子随机抽取1个小球,取到标号为2的小球的概率是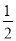 ,可求n的值; (2)①从袋子中不放回地随机抽取2个球,共有基本事件12个,其中“a+b=2”为事件A的基本事件有4个,故可求概率;
,可求n的值; (2)①从袋子中不放回地随机抽取2个球,共有基本事件12个,其中“a+b=2”为事件A的基本事件有4个,故可求概率;
②记“x2+y2>(a-b)2恒成立”为事件B,则事件B等价于“x2+y2>4恒成立, (x,y)可以看成平面中的点,确定全部结果所构成的区域,事件B构成的区域,即可求得结论.
试题解析:(1)由题意可知,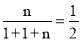 ,解得n=2.
,解得n=2.
(2)①不放回地随机抽取2个小球的所有基本事件为(0,1),(0,21),(0,22),(1,0),(1,21),(1,22),(21,0),(21,1),(21,22),(22,0),(22,1),(22,21),共12个.
事件A包含的基本事件为(0,21),(0,22),(21,0),(22,0),共4个,所以P(A)=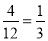 .
.
②记“x2+y2>(a-b)2恒成立”为事件B,则事件B等价于“x2+y2>4”,(x,y)可以看成平面中的点,则全部结果所构成的区域Ω={(x,y)|0≤x≤2,0≤y≤2,x,y∈R},而事件B所构成的区域B={(x,y)|x2+y2>4,(x,y)∈Ω},所以P(B)=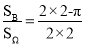 =1-
=1-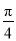 .
.
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
