如图甲所示，两根光滑固定导轨相距0.4m竖直放置，导轨电阻不计，在导轨末端P、Q两点用两根等长的细导线悬挂金属棒cd.棒cd的质量为0.01kg，长为0.2 m，处于磁感应强度为B0＝0.5T的匀强磁

如图甲所示，两根光滑固定导轨相距0.4m竖直放置，导轨电阻不计，在导轨末端P、Q两点用两根等长的细导线悬挂金属棒cd.棒cd的质量为0.01kg，长为0.2 m，处于磁感应强度为B0＝0.5T的匀强磁场中，磁场方向垂直于导轨平面向里．相距0.2 m的水平虚线MN和JK之间的区域内存在着垂直于导轨平面向里的匀强磁场，且磁感应强度B随时间变化的规律如图乙所示．在t＝0时刻，质量为0.02kg、阻值为0.3Ω的金属棒ab从虚线MN上方0.2m高度处，由静止开放释放，下落过程中保持水平，且与导轨接触良好，结果棒ab在t1时刻从上边界MN进入磁场，并在磁场中做匀速运动，在t2时刻从下边界JK离开磁场，g取10 m/s2.求：

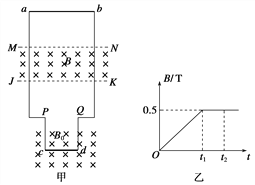
(1)在0～t1时间内，电路中感应电动势的大小；

(2)在t1～t2时间内，棒cd受到细导线的总拉力为多大；

(3)棒cd在0～t2时间内产生的焦耳热．

【答案】

(1) E1＝0.2V (2)FT＝0.2 N (3)Qcd＝0.015J

【解析】

(1)对棒ab自由下落过程，有t1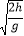＝＝0.2 s

磁感应强度的变化率为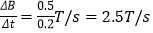

由法拉第电磁感应定律得，0～t1时间内感应电动势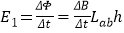

联立以上各式并代入数据可得E1＝0.2V

(2)由棒ab匀速进入磁场区域可知BI2Lab＝mabg

代入数据，可解得I2＝1A

在t1～t2时间内，对棒cd受力分析，可得FT＝mcdg＋B0I2Lcd

代入数据，可解得FT＝0.2 N

(3)棒ab刚进入磁场时的速度为v＝gt1＝2 m/s

棒ab刚进入磁场后的感应电动势为E2＝BLabv＝0.4 V

则Rcd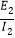＝－Rab＝0.1 Ω

在0～t1时间内，感应电流为I1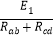＝＝0.5 A

棒cd在0～t2时间内产生的焦耳热Qcd＝Q1＋Q2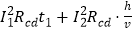＝＝0.015 J．