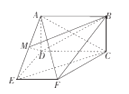
如图，矩形ABCD所在平面与直角梯形CDEF所在平面互相垂直，其中∠EDC=∠DEF=<img alt="1" src="/tk/20210512/16207510

如图，矩形ABCD所在平面与直角梯形CDEF所在平面互相垂直，其中∠EDC=∠DEF= ， EF=ED=CD=1，AD= ．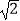

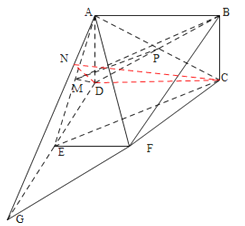
（1）若M为AE的中点，求证：EC∥平面BDM；

（2）求平面ADE与平面ACF所成锐二面角的大小．

【答案】

（1）证明（1）连接：设AC交BD于P，连接PM．

三角形ACE中，M为AE中点，P为AC中点，

∴CE∥PM．

∵PM⊂平面BDM中，CM⊄平面BDM中，

∴CE∥平面BDM．

（2）延长CF和DE交于G，连接AG．作三角形AG边上的高DN，连接CN．

∵CD⊥AD，CD⊥DG，

∴CD⊥平面ADG，

∵AG⊂平面ADG，

故CD⊥AG．

∵DN⊥AG，

∴AG⊥平面CDN．

则CN⊥AG．

则∠CND是二面角的平面角，

∵EF=ED=CD=1，AD=．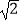

∴DG=2，AG=．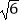

∵sin∠DGN=，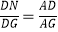

∴DN=．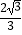

则tan∠CND==，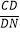

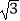故∠CND=60°．

即平面ADE与平面ACF所成锐二面角的大小60°．

【解析】

（1）若M为AE的中点，根据线面平行的判定定理即可证明EC∥平面BDM；

（2）根据二面角的定义作出二面角的平面角，结合三角形的边角关系即可求平面ADE与平面ACF所成锐二面角的大小．

【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行．