已知函数 <img alt="1" src="/tk/20210512/1620751591550.png"/><img alt="

已知函数 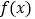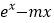 （ m 为常数）．

（Ⅰ）若曲线 y f  x 在点 0, f 0 处的切线斜率为 1 ，求实数 m 的值．

（Ⅱ）求函数 f x  的极值．

（Ⅲ）证明：当 x 0 时，．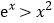

【答案】

（1）m = 2 ；（2）f (x)的极小值为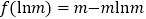，无极大值；（3）证明见解析.

【解析】

（Ⅰ）求出f′（x）=ex﹣m，（m∈R），f′（0）=1﹣m，利用导数的几何意义能求出m；（Ⅱ）由f′（x）=ex﹣m，（m∈R），函数f（x）定义域为（﹣∞，+∞），利用导数性质能求出f（x）的极值；（Ⅲ）设函数g（x）=ex﹣x2，则g′（x）=ex﹣2x，当m=2时，g′（x）=f（x）≥f（ln2），由g′（x）＞0恒成立，能证明ex＞x2．

（Ⅰ）∵函数f（x）=ex﹣mx（m为常数），

∴f′（x）=ex﹣m，（m∈R），∴f′（0）=1﹣m，

∵曲线y=f（x）在点（0，f（0））的切线斜率为﹣1，

∴f′（0）=1﹣m=﹣1，

解得m=2．

（Ⅱ）∵f′（x）=ex﹣m，（m∈R），

函数f（x）定义域为（﹣∞，+∞），

当m≤0时，f′（x）＞0，函数f（x）在（﹣∞，+∞）上单调递增，

此时没有极值；

当m＞0时，令f′（x）=0，解得x=lnm，

则随着x的变化，f′（x），f（x）变化如下表：

x

（﹣∞，lnm）

lnm

（lnm，+∞）

f′（x）

﹣

0

+

f（x）

↓

极小值

↑

由上表知函数f（x）在（lnm，+∞）上单调递增，在（﹣∞，lnm）上单调递减，

则在x=lnm处取得极小值f（lnm）=elnm﹣mlnm=m（1﹣lnm），

无极大值．

证明：（Ⅲ）设函数g（x）=ex﹣x2，

则g′（x）=ex﹣2x，

由（Ⅱ）知m=2时，g′（x）=f（x）≥f（ln2），

∵f（ln2）=2（1﹣ln2）＞0，∴g′（x）＞0恒成立，

即函数g（x）在R上递增，

∵g（0）=1，∴当x＞0时，g（x）＞g（0）＞0，

∴ex＞x2．