如图，四棱锥P﹣ABCD的底面ABCD是平行四边形，BA=BD=<img alt="1" src="/tk/20210512/1620750817591.png&q

如图，四棱锥P﹣ABCD的底面ABCD是平行四边形，BA=BD=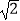 ， AD=2，PA=PD= 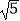， E，F分别是棱AD，PC的中点．证明EF∥平面PAB

【答案】

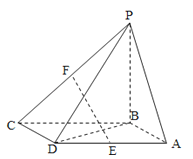
解：证明：连结AC，AC∩BD=H，

∵底面ABCD是平行四边形，∴H为BD中点，

∵E是棱AD的中点．∴在△ABD中，EH∥AB，

又∵AB⊂平面PAB，EH⊄平面PAD，∴EH∥平面PAB．

同理可证，FH∥平面PAB．

又∵EH∩FH=H，∴平面EFH∥平面PAB，

∵EF⊂平面EFH，∴EF∥平面PAB

【解析】

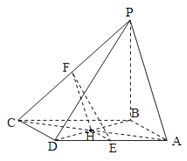
要证明EF∥平面PAB，可以先证明平面EFH∥平面PAB，而要证明面面平行则可用面面平行的判定定理来证.

【考点精析】根据题目的已知条件，利用直线与平面平行的判定的相关知识可以得到问题的答案，需要掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行．