设P是不等式组<img alt="1" src="/tk/20210512/1620751870390.png"/>表示的平面区域内的任意一点，向量
设P是不等式组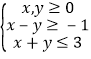
表示的平面区域内的任意一点，向量
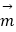=(1,1),
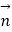=(2,1)，若
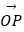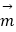=λ+μ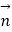 ， 则2λ+μ的最大值为______
5
【解析】∵向量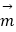
=(1,1),
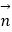=(2,1)，且
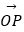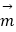=λ+μ ，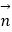
∴P（x，y）满足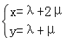
， 代入不等式组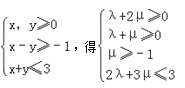
作出不等式组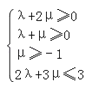
表示的平面区域，
得到如图的四边形OABC及其内部，
其中A（﹣3，3），B（3，﹣1），C（2，﹣1），O为坐标原点
设z=F（λ，μ）=2λ+μ，将直线l：z=2λ+μ进行平移，
可得当l经过点B时，目标函数z达到最大值
∴z最大值=F（3，﹣1）=2×3+（﹣1）=5
所以答案是：5
版权声明
声明：有的资源均来自网络转载，版权归原作者所有，如有侵犯到您的权益
请联系本站我们将配合处理！