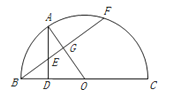
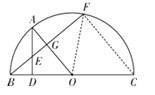
如图所示，BC是半圆O的直径，AD⊥BC，垂足为D，<img alt="1" src="/tk/20210512/1620750907188.png"/&

如图所示，BC是半圆O的直径，AD⊥BC，垂足为D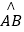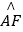，= ， BF与AD、AO分别交于点E、G．

（1）证明：∠DAO=∠FBC；

（2）证明：AE=BE．

【答案】

证明：（Ⅰ）连接FC，OF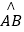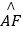，∵=，OB=OF，∴点G是BF的中点，OG⊥BF．

因为BC是⊙O的直径，所以CF⊥BF．∴OG∥CF．∴∠AOB=∠FCB，

∴∠DAO=90°﹣∠AOB，∠FBC=90°﹣∠FCB，∴∠DAO=∠FBC．

（Ⅱ）在Rt△OAD与Rt△OBG中，由（Ⅰ）知∠DAO=∠GBO，

又OA=OB，所以，△OAD≌△OBG，于是OD=OG．

∴AG=OA﹣OG=OB﹣OD=BD．

在Rt△AGE与Rt△BDE中，由于∠DAO=∠FBC，AG=BD，

所以，△AGE≌△BDE，因此，AE=BE．

【解析】

（Ⅰ）连接FC，OF，利用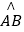= 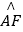， 说明OB=OF，然后证明∠AOB=∠FCB，推出∠DAO=∠FBC．

（Ⅱ）证明△OAD≌△OBG，推出OD=OG．然后证明△AGE≌△BDE，即可证明AE=BE．