四边形ABCD是菱形，∠BAD=60°，AB=6，对角线AC与BD相交于点O，点E在AC上，若OE=<img alt="1" src="/tk/20210512/1
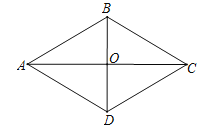
四边形ABCD是菱形，∠BAD=60°，AB=6，对角线AC与BD相交于点O，点E在AC上，若OE=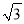
，则CE的长为______．
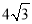或
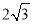
解：∵四边形ABCD是菱形，∴AB=AD=6，AC⊥BD，OB=OD，OA=OC，∵∠BAD=60°，∴△ABD是等边三角形，∴BD=AB=6，∴OB=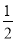
BD=3，∴OC=OA=
=
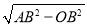，∴AC=2OA=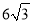
，∵点E在AC上，OE=
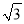，∴CE=OC+
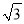或CE=OC﹣
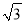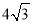，∴CE=
或CE=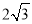
；故答案为：
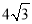或
．
版权声明
声明：有的资源均来自网络转载，版权归原作者所有，如有侵犯到您的权益
请联系本站我们将配合处理！