已知函数f（x）=<img alt="1" src="/tk/20210512/1620750864602.png"/>x3+bx2+cx+d，设曲

已知函数f（x）=x3+bx2+cx+d，设曲线y=f（x）在与x轴交点处的切线为y=4x﹣12，f′（x）为f（x）的导函数，满足f′（2﹣x）=f′（x）．

（Ⅰ）求f（x）的解析式．

（Ⅱ）若函数在区间（m，n）内的图象从左到右的单调性为依次为减﹣增﹣减﹣增，则称该函数在区间（m，n）内是“W﹣型函数”．已知函数g（x）=（x2+k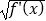）•在区间（﹣1，2）内是“W﹣型函数”，求实数k的取值范围．

【答案】

解：（1）∵f（x）=x3+bx2+cx+d，

∴f′（x）=x2+2bx+c，

∵f′（2﹣x）=f′（x），

∴函数y=f′（x）的图象关于直线x=1对称，则b=﹣1．

∵直线y=4x﹣12与x轴的交点为（3，0），

∴f（3）=0，且f′（3）=4，即9+9b+3c+d=0①，且9+6b+c=4②，由①②解得c=1，d=﹣3．

∴

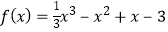
（2）∵f′（x）=x2﹣2x+1=（x﹣1）2 ，

∴g（x）=（x2+k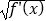）•=（x2+k）•|x﹣1|=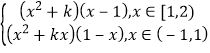

当x∈[1，2）时，g′（x）=3x2﹣2x+k，

当x∈（﹣1，1）时，g′（x）=﹣3x2+2x﹣k，

①若g'（x）=0在（﹣1，1）上有两根，且g'（x）≥0对x∈[1，2）恒成立

当x∈（﹣1，1）时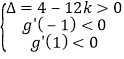，且x∈[1，2）时，g'（1）≥0，

解得：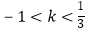

②若g'（x）=0在（﹣1，1）上有一根，且g'（x）=0在x∈[1，2）上有一根

x∈（﹣1，1）时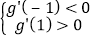，且x∈[1，2）时，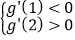

解得：﹣5＜k＜﹣1

③若g'（x）≤0在（﹣1，1）上恒成立，且g'（x）=0在x∈[1，2）上有两根

而x∈[1，2）时，g'（x）=3x2﹣2x+k对称轴为x=，所以不可能有两根，舍去．

综上：﹣5＜k＜﹣1或

【解析】

（1）由f′（2﹣x）=f′（x）可得其对称轴x=1，据此可得b值，求出直线y=4x﹣12与x轴交点（3，0），则f（3）=0，且f′（3）=4，从而可解得c、d值，根据f′（x）的符号即可求得函数的单调区间；

（2）利先求出g（x），求导，然后根据“W﹣型函数”，转化为方程再区间的上的根的问题，问题得以解决．

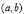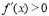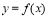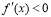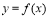【考点精析】通过灵活运用利用导数研究函数的单调性，掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减即可以解答此题．