已知抛物线y1＝x2与直线y2＝－<img alt="1" src="/tk/20210512/1620768543376.png"/>x＋3相交于
已知抛物线y1＝x2与直线y2＝－
x＋3相交于A，B两点．
(1)求这两个交点的坐标；
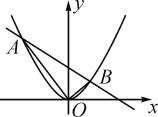
(2)点O的坐标是原点，求△AOB的面积；
(3)直接写出当y1＜y2时，x的取值范围．
(1) A(－2，4)，B(
，
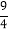) ； (2) S△AOB＝
；(3)－2＜x＜.
（1）根据解方程组，可得交点坐标；
（2）根据面积的和差，可得答案；
（3）根据函数与不等式的关系，可得答案．
（1）联立抛物线y1=x2与直线y2=-
x+3，得
，
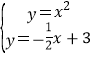解得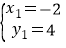
，
，
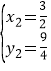A（-2，4），B（
，
）；
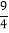（2）如图，
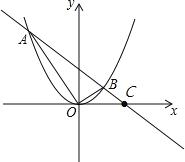
当y=0时，-x+3=0，解得x=6，
即C（6，0）．
S△AOB=S△AOC-S△BOC=×6×4-×6×=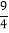
；
（3）抛物线在直线的下方，得-2＜x＜．
版权声明
声明：有的资源均来自网络转载，版权归原作者所有，如有侵犯到您的权益
请联系本站我们将配合处理！