在直角坐标系xOy中,过点P(1,﹣2)的直线l的倾斜角为45°.以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=2cosθ,直线l和曲线C的交点为点A、B.
在直角坐标系xOy中,过点P(1,﹣2)的直线l的倾斜角为45°.以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=2cosθ,直线l和曲线C的交点为点A、B.
(I)求直线l的参数方程;
(Ⅱ)求|PA|•|PB|的值.
【答案】解:(1)在直角坐标系xOy中,过点P(1,﹣2)的直线l的倾斜角为45°.
∴kl=1,直线方程是:y+2=x﹣1,y=x﹣3,
令x=t,则y=t﹣3,
∴直线l的参数方程是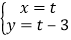 ;
;
(2)以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,
曲线C的极坐标方程为ρsin2θ=2cosθ,
即为ρ2sin2θ=2ρcosθ,
化为普通方程为:y2=2x,
由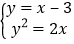 ,
,
解得: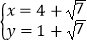 或
或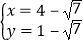 ,
,
∴|PA|•|PB|=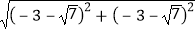 •
•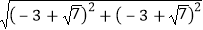 =4.
=4.
(1)求出直线的普通方程,令x=t,从而求出直线的参数方程;
(2)求出曲线C的普通方程,联立方程组,求出A、B的坐标,根据两点间的距离公式求出|PA|•|PB|的值即可.
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
