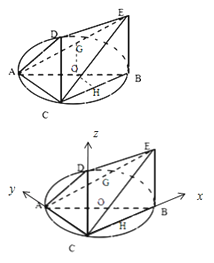
如图，一简单几何体ABCDE的一个面ABC内接于圆O，G、H分别是AE、BC的中点，AB是圆O的直径，四边形DCBE为平行四边形，且DC⊥平面ABC．

如图，一简单几何体ABCDE的一个面ABC内接于圆O，G、H分别是AE、BC的中点，AB是圆O的直径，四边形DCBE为平行四边形，且DC⊥平面ABC．

（Ⅰ）证明：GH∥平面ACD；

（Ⅱ）若AC=BC=BE=2，求二面角O﹣CE﹣B的余弦值．

【答案】

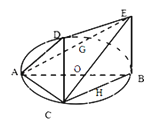
解：（Ⅰ）证明：连结GO，OH

∵GO∥AD，OH∥AC…（2分）

∴GO∥平面ACD，OH∥平面ACD，又GO交HO于O…（.4分）

∴平面GOH∥平面ACD…（5分）

∴GH∥平面ACD…（6分）

（Ⅱ）以CB为x轴，CA为y轴，CD为z轴，建立如图所示的直角坐标系

则C（0，0，0），B（2，0，0），A（0，2，0），O（1，1，0），E（2，0，2）

平面BCE的法向量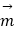=（0，1，0），设平面OCE的法向量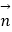=（x0 ． y0 ． z0）．…（8分）

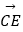=（2，0，2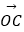），=（1，1，0）．

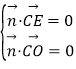∴则，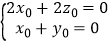

令x0=﹣1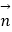，∴=（﹣1，1，1）．…（10分）

∵二面角O﹣CE﹣B是锐二面角，记为θ，则

cosθ=|cos<,>|===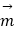

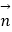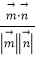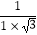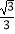
【解析】

（Ⅰ）连结GO，OH，证明GO∥平面ACD，OH∥平面ACD，利用平面与平面平行的判定定理证明平面GOH∥平面ACD．然后证明GH∥平面ACD．

（Ⅱ）以CB为x轴，CB为y轴，CD为z轴，建立如图所示的直角坐标系，求出C，B，A（，O，E的坐标，平面BCE的法向量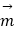 ， 平面OCE的法向量 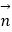． 二面角O﹣CE﹣B是锐二面角，记为θ，利用空间向量的数量积求解cosθ即可。