已知函数f(x)=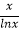 +ax,x>1.
+ax,x>1.
(Ⅰ)若f(x)在(1,+∞)上单调递减,求实数a的取值范围;
(Ⅱ)若a=2,求函数f(x)的极小值;
(Ⅲ)若方程(2x﹣m)lnx+x=0在(1,e]上有两个不等实根,求实数m的取值范围.
【答案】解:(Ⅰ)函数f(x)=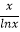 +ax,x>1.
+ax,x>1.
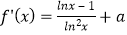 ,由题意可得f′(x)≤0在x∈(1,+∞)上恒成立;
,由题意可得f′(x)≤0在x∈(1,+∞)上恒成立;
∴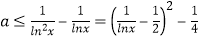 ,
,
∵x∈(1,+∞),∴lnx∈(0,+∞),
∴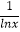 -
- =0时函数t=(
=0时函数t=(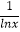 -
- )2-
)2- 的最小值为-
的最小值为- ,
,
∴a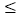 -
-
(Ⅱ) 当a=2时,f(x)=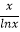 +2x
+2x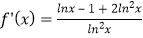
令f′(x)=0得2ln2x+lnx﹣1=0,
解得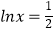 或lnx=﹣1(舍),即x=
或lnx=﹣1(舍),即x=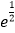
当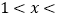
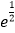 时,f'(x)<0,当x>
时,f'(x)<0,当x>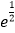 时,f′(x)>0
时,f′(x)>0
∴f(x)的极小值为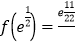 =2
=2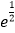 =4
=4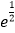
(Ⅲ)将方程(2x﹣m)lnx+x=0两边同除lnx得(2x-m)+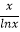 =0
=0
整理得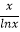 +2x=m
+2x=m
即函数f(x)与函数y=m在(1,e]上有两个不同的交点;
由(Ⅱ)可知,f(x)在(1,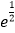 )上单调递减,在(
)上单调递减,在(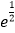 ,e)上单调递增f(
,e)上单调递增f(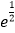 )=4
)=4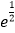 ,f(e)=3e,当x→1时,
,f(e)=3e,当x→1时,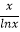
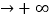 ,∴4
,∴4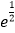
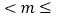 3e,
3e,
实数m的取值范围为(4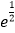 ,3e)
,3e)
(Ⅰ)求出函数的导数,通过f′(x)≤0在x∈(1,+∞)上恒成立,得到a的不等式,利用二次函数的求出最小值,得到a的范围.
(Ⅱ)利用a=2,化简函数的解析式,求出函数的导数,然后求解函数的极值.
(Ⅲ)化简方程(2x﹣m)lnx+x=0,得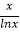 +2x=m,利用函数f(x)与函数y=m在(1,e]上有两个不同的交点,结合由(Ⅱ)可知,f(x)的单调性,推出实数m的取值范围.
+2x=m,利用函数f(x)与函数y=m在(1,e]上有两个不同的交点,结合由(Ⅱ)可知,f(x)的单调性,推出实数m的取值范围.
【考点精析】利用利用导数研究函数的单调性和函数的极值与导数对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间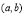 内,(1)如果
内,(1)如果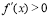 ,那么函数
,那么函数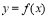 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果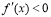 ,那么函数
,那么函数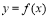 在这个区间单调递减;求函数
在这个区间单调递减;求函数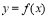 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在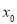 附近的左侧
附近的左侧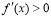 ,右侧
,右侧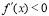 ,那么
,那么 是极大值(2)如果在
是极大值(2)如果在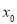 附近的左侧
附近的左侧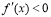 ,右侧
,右侧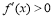 ,那么
,那么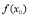 是极小值.
是极小值.
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
