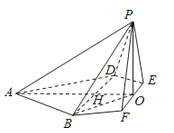
如图1，在边长为4的菱形ABCD中，∠DAB=60°，点E，F分别是边CD，CB的中点，AC∩EF=O．沿EF将△CEF翻折到△PEF，连接PA，PB，PD，得到如图2的五棱锥P﹣ABFED，且PB=

如图1，在边长为4的菱形ABCD中，∠DAB=60°，点E，F分别是边CD，CB的中点，AC∩EF=O．沿EF将△CEF翻折到△PEF，连接PA，PB，PD，得到如图2的五棱锥P﹣ABFED，且PB= ．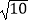

（1）求证：BD⊥平面POA；

（2）求四棱锥P﹣BFED的体积．

【答案】

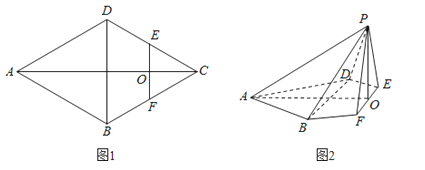
（1）证明：如图，

∵点E，F分别是边CD，CB的中点，

∴BD∥EF．

∵菱形ABCD的对角线互相垂直，

∴BD⊥AC．

∴EF⊥AC．

∴EF⊥AO，EF⊥PO．

∵AO⊂平面POA，PO⊂平面POA，AO∩PO=O，

∴EF⊥平面POA．

∴BD⊥平面POA．

（2）解：设AO∩BD=H，连接BO，

∵∠DAB=60°，

∴△ABD为等边三角形．

∴BD=4，BH=2，HA=2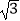，HO=PO=．

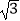在Rt△BHO中，BO==，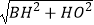

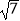在△PBO中，BO2+PO2=10=PB2 ，

∴PO⊥BO．

∵PO⊥EF，EF∩BO=O，EF⊂平面BFED，BO⊂平面BFED，

∴PO⊥平面BFED．

梯形BFED的面积为S=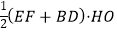=3，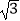

∴四棱锥P﹣BFED的体积V=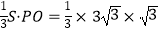=3．

【解析】

（1）由三角形的中位线定理可证BD∥EF，再由菱形的对角线互相垂直证得BD⊥AC．即可得到EF⊥AO，再由已知可得EF⊥PO，然后利用线面垂直的判定得答案；

（2）设AO∩BD=H，连接BO，结合已知可得HO=PO=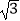 ， 通过解直角三角形求得PO⊥平面BFED．然后求出梯形BFED的面积，代入棱锥的体积公式得答案．