已知函数f(x)=2<img alt="1" src="/tk/20210512/1620750866013.png"/>sinxcosx+2cos
已知函数f(x)=2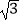 sinxcosx+2cos2x+m在区间[0,
sinxcosx+2cos2x+m在区间[0, ]上的最大值为2.求常数m的值;
]上的最大值为2.求常数m的值;
解:f(x)=2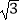 sinxcosx+2cos2x+m=2sin(2x+
sinxcosx+2cos2x+m=2sin(2x+ )+m+1,
)+m+1,
∵x∈[0, ],∴2x+
],∴2x+ ∈[
∈[ ,
,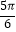 ],
],
∴当2x+ =
= 即x=
即x= 时,函数f(x)在区间[0,
时,函数f(x)在区间[0, ]上取到最大值,
]上取到最大值,
此时,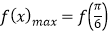 =m+3=2,解得m=﹣1
=m+3=2,解得m=﹣1
先化简得f(x)=2sin(2x+ )+m+1,由x的范围可求得函数最大值,令其等于2可求m.
)+m+1,由x的范围可求得函数最大值,令其等于2可求m.
【考点精析】关于本题考查的正弦定理的定义,需要了解正弦定理: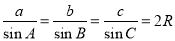 才能得出正确答案.
才能得出正确答案.
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
