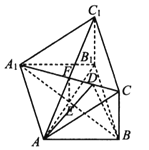
如图所示,在三棱柱<img alt="1" src="/tk/20210511/1620712458663.png"/>中,四边形<img a
如图所示,在三棱柱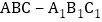 中,四边形
中,四边形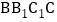 是长方形,
是长方形,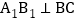 ,
,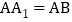 ,
,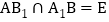 ,
,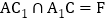 ,连接
,连接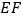 .
.
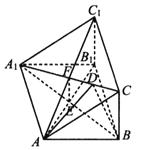
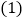 证明:平面
证明:平面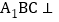 平面
平面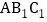 ;
;
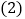 若
若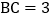 ,
,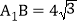 ,
,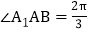 ,
,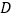 是线段
是线段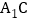 上的一点,且
上的一点,且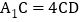 ,试求
,试求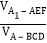 的值.
的值.
(1)见解析;(2)1
【解析】 先证明
先证明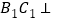 平面
平面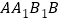 ,连结
,连结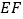 ,可得
,可得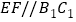 ,推导出
,推导出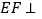 平面
平面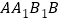 ,从而
,从而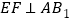 ,进而平行四边形
,进而平行四边形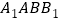 是菱形,由菱形的性质得对角线
是菱形,由菱形的性质得对角线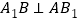 ,从而
,从而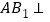 平面
平面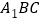 ,从而可得结果;
,从而可得结果;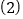 先证明
先证明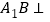 平面
平面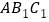 ,得
,得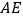 的长为三棱锥
的长为三棱锥 的高,
的高,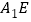 的长为三棱锥
的长为三棱锥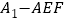 的高,由余弦定理得
的高,由余弦定理得 ,从而
,从而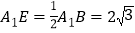 ,
,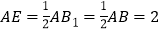 ,推导出
,推导出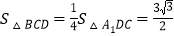 ,由此能求出
,由此能求出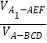 的值.
的值.
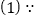 在三棱柱
在三棱柱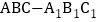 中,
中,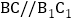 ,
,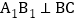 ,
,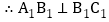 ,
,
又在长方形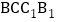 中,
中,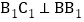 ,
,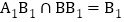 ,
,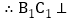 平面
平面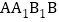 ,
,
 四边形
四边形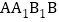 与四边形
与四边形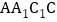 均是平行四边形,
均是平行四边形,
且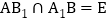 ,
,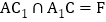 ,连结EF,
,连结EF,
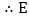 为
为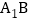 的中点,F为
的中点,F为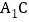 的中点,EF为
的中点,EF为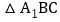 的中位线,
的中位线,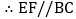 ,
,
又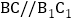 ,
,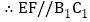 ,又
,又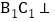 平面
平面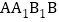 ,
, 平面
平面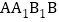 ,
,
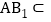 平面
平面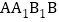 ,
,
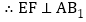 ,又在平行四边形
,又在平行四边形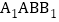 中,
中,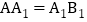 ,
,
 平行四边形
平行四边形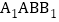 是菱形,
是菱形,
由菱形的性质得对角线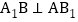 ,
,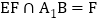 ,
,
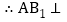 平面
平面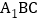 ,又
,又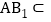 平面
平面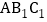 ,
,
 平面
平面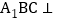 平面
平面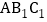 .
.
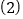 由
由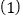 知
知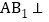 平面
平面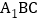 ,
,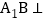 平面
平面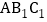 ,
,
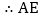 的长为三棱锥
的长为三棱锥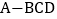 的高,
的高,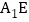 的长为三棱锥
的长为三棱锥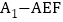 的高,
的高,
 在菱形
在菱形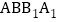 中,
中,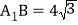 ,
,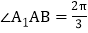 ,
,
 在
在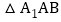 中,由余弦定理得
中,由余弦定理得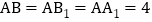 ,
,
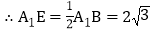 ,
,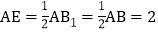 ,
,
又在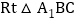 中,
中,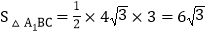 ,
,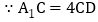 ,
,
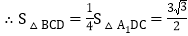 ,
,
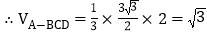 ,
,
又在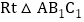 中,
中,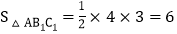 ,
,
又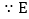 ,F分别为
,F分别为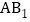 ,
,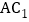 中点,
中点,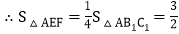 ,
,
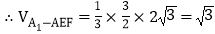 ,
,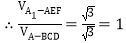 .
.
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
