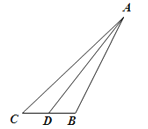
如图，在△ABC中，∠C=45°，D为BC中点，BC=2，记锐角∠ADB=α．且满足cos2α=﹣<img alt="1" src="/tk/20210512/16

如图，在△ABC中，∠C=45°，D为BC中点，BC=2，记锐角∠ADB=α．且满足cos2α=﹣ ．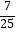

（1）求cos∠CAD；

（2）求BC边上的高h的值．

【答案】

解（1）∵cos2α=2cos2α﹣1=﹣，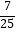

∴cos2α=，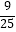

∵α∈（0，），

∴cosα=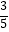，sinα=，

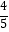∵∠CAD=α﹣45°，

∴cos∠CAD=cos（α﹣45°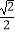）=（cosα+sinα）=；

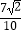（2）由（1）得，sin∠CAD==，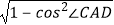

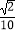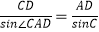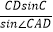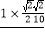在△ACD中，由正弦定理得：，即AD===5，

则高h=ADsin∠ADB=4．

【解析】

（1）已知等式利用二倍角的余弦函数公式化简，求出cosα的值，利用外角性质表示出∠CAD，利用两角和与差的余弦函数公式化简，把各自的值代入计算即可求出值；

（2）由cos∠CAD的值求出sin∠CAD的值，再由sinC以及CD的长，利用正弦定理求出AD的长，再利用锐角三角函数定义求出h的值即可．

【考点精析】认真审题，首先需要了解两角和与差的正弦公式(两角和与差的正弦公式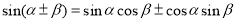：)，还要掌握正弦定理的定义(正弦定理: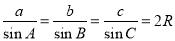)的相关知识才是答题的关键．