如图，在平面直角坐标系xOy中，函数y=<img alt="1" src="/tk/20210512/1620768380861.png"/>（k＞

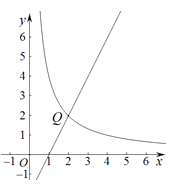
如图，在平面直角坐标系xOy中，函数y=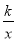（k＞0，x＞0）的图象与直线y=2x﹣2交于点Q（2，m）．

（1）求m，k的值；

（2）已知点P（a，0）（a＞0）是x轴上一动点，过点P作平行于y轴的直线，交直线y=2x﹣2于点M，交函数y=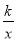的图象于点N．

①当a=4时，求MN的长；

②若PM＞PN，结合图象，直接写出a的取值范围．

【答案】

（1）m=2，k=4；（2）①MN=5；②a＞2．

【解析】

（1）把Q（2，m）代入y=2x﹣2，求出m的值，再把求得的Q（2，2）代入y=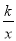，可求出k的值；

（2）①把a=4分别代入y=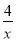和y=2x﹣2中，求出点M和点N的纵坐标，从而可求出MN的长度；②由图像可知，当a>2时，PM>PN.

解：（1）∵直线y=2x﹣2经过点Q（2，m），∴m=2，∴Q（2，2）．

∵函数y=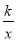经过点Q（2，2），∴k=4．

（2）①当a=4时，P（4，0）．

∵y=2x﹣2，y=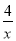，∴M（4，6），N（4，1），∴MN=5．

②∵PM＞PN，∴a＞2．