已知f(x)=<img alt="1" src="/tk/20210512/1620760656302.png"/>是定义在[-1,1]上的奇函数,
已知f(x)=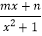 是定义在[-1,1]上的奇函数,且f(-
是定义在[-1,1]上的奇函数,且f(-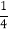 )=
)=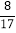 .
.
(1)求f(x)的解析式;
(2)用单调性的定义证明:f(x)在[-1,1]上是减函数.
【答案】(1)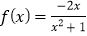 ;(2)详见解析.
;(2)详见解析.
(1)由奇函数的性质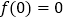 ,即得
,即得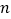 值,又由
值,又由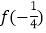 ,解可得
,解可得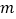 的值,将
的值,将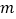 、
、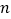 的值代入
的值代入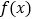 的解析式,计算可得答案;
的解析式,计算可得答案;
(2)根据题意,由作差法证明即可得结论.
解:(1)根据题意,f(x)=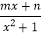 是定义在[-1,1]上的奇函数,且f(-
是定义在[-1,1]上的奇函数,且f(-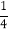 )=
)=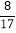 ,
,
则f(0)=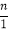 =0,即n=0,则f(x)=
=0,即n=0,则f(x)=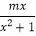 ,
,
又由f(-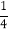 )=
)=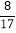 ,则f(-
,则f(-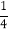 )=
)=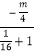 =
=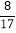 ,解可得m=-2,
,解可得m=-2,
则f(x)=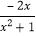 ;
;
(2)函数f(x)在[-1,1]上为减函数,
证明:设-1≤x1<x2≤1,
f(x1)-f(x2)=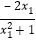 -
-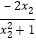 =
=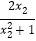 -
-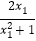 =2×
=2×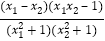 ,
,
又由-1≤x1<x2≤1,
则(x1-x2)<0,x1-x2-1<0,(x12+1)>0,(x22+1)>0,
则f(x1)-f(x2)>0,
则函数f(x)在[-1,1]上是减函数.
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
