已知函数f(x)=sin(x﹣<img alt="1" src="/tk/20210512/1620750868322.png"/>)+cosx.
已知函数f(x)=sin(x﹣ )+cosx.
)+cosx.
(1)求函数f(x)的最小正周期;
(2)若α是第一象限角,且f(α+ )=
)=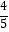 , 求tan(α﹣
, 求tan(α﹣ )的值.
)的值.
解:(1)f(x)=sin(x﹣ )+cosx
)+cosx
=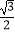 sinx-
sinx- cosx+cosx
cosx+cosx
=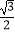 sinx+
sinx+ cosx
cosx
=sin(x+ )
)
所以:函数f(x)的最小正周期为:T=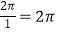
(2)由于f(x)=sin(x+ )
)
则:f(α+ )=sin(α+
)=sin(α+ )=cosα=
)=cosα=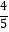
由于α是第一象限角
所以:sinα=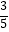
则: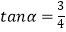
则:tan(α﹣ )=
)=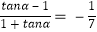
(1)首先对三角函数关系式进行恒等变换,把函数关系式变形成正弦型函数,进一步求出函数的最小正周期.
(2)利用(1)求出的函数关系式,进一步求出函数的正弦值和余弦值,进一步求出函数的正切值,最后求出结果.
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
