在△ABC中，a ， b ， c分别为∠A ， ∠B ， ∠C的对边．如果a ， b ， c成等差数列，∠B＝30°，△ABC的面积为<img alt="1" src=&qu
在△ABC中，a ， b ， c分别为∠A ， ∠B ， ∠C的对边．如果a ， b ， c成等差数列，∠B＝30°，△ABC的面积为
， 那么b＝( )．
A.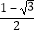
B.
C.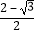
D.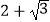
B
【解析】根据等差中项的性质可知2b=a+c．平方后整理得a2+c2=4b2-2ac．利用三角形面积求得ac的值，进而把a2+c2=4b2-2ac．代入余弦定理求得b的值．：∵a，b，c成等差数列，∴2b=a+c．平方得a2+c2=4b2-2ac．又△ABC的面积为
， 且∠B=30°，故由S△=
acsinB=ac•sin30°=
ac= ， 得ac=6，∴a2+c2=4b2-12．由余弦定理
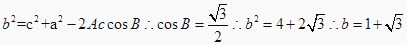,故选B
版权声明
声明：有的资源均来自网络转载，版权归原作者所有，如有侵犯到您的权益
请联系本站我们将配合处理！