在平面直角坐标系xoy中，以O为极点，x轴的正半轴为极轴的极坐标系中，直线l的极坐标方程为θ=<img alt="1" src="/tk/20210512/1620

在平面直角坐标系xoy中，以O为极点，x轴的正半轴为极轴的极坐标系中，直线l的极坐标方程为θ= ， 曲线C的参数方程为 ．

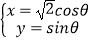（1）写出直线l与曲线C的直角坐标方程；

（2）过点M平行于直线l1的直线与曲线C交于A、B两点，若|MA|•|MB|= ， 求点M轨迹的直角坐标方程．

【答案】

解：（1）直线l的极坐标方程为θ=，所以直线斜率为1，直线l：y=x；

曲线C的参数方程为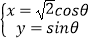．消去参数θ，

可得曲线C: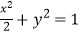

（2）设点M（x0 ， y0）及过点M的直线为l: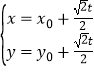

由直线l1与曲线C相交可得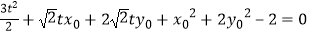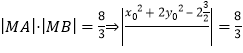：，即：，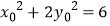

x2+2y2=6表示一椭圆

取y=x+m代入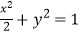得：3x2+4mx+2m2﹣2=0

由△≥0得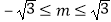

故点M的轨迹是椭圆x2+2y2=6夹在平行直线y=x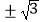之间的两段弧

【解析】

（1）利用极坐标与直角坐标方程的互化，直接写出直线l的普通方程，消去参数可得曲线C的直角坐标方程；

（2）设点M（x0 ， y0）以及平行于直线l1的直线参数方程，直线l1与曲线C联立方程组，通过|MA|•|MB|= ， 即可求点M轨迹的直角坐标方程．通过两个交点推出轨迹方程的范围，