当代物理理论认为:当一个体系的势能最小时,系统会处于稳定平衡状态,这个规律称为“最小势能原理”。如图甲所示,两个带正电的小球A、B套在一个倾斜的光滑直杆上,两球均可视为点电荷,其中A球固定,带电量QA
当代物理理论认为:当一个体系的势能最小时,系统会处于稳定平衡状态,这个规律称为“最小势能原理”。如图甲所示,两个带正电的小球A、B套在一个倾斜的光滑直杆上,两球均可视为点电荷,其中A球固定,带电量QA=2×10﹣4C,B球的质量为m=0.1kg.以A为坐标原点,沿杆向上建立直线坐标系如乙图,B球的总势能随位置x的变化规律如图中曲线Ⅰ所示,直线Ⅱ为曲线I的渐近线,P点为曲线Ⅰ的最低点,坐标为(6m、6J),Q点坐标为(2m、10J).甲图中M点离A点距离为6m.(g取10m/s2,静电力恒量k=9.0×109N•m2/C2.)
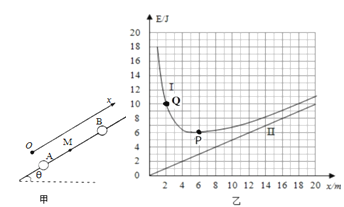
(1)求杆与水平面的夹角θ;
(2)求B球的带电量QB;
(3)求M点电势φM;
(4)若B球以Ek0=4J的初动能从M点开始沿杆向上滑动,求B球运动过程中离A球的最近距离及此时B球的加速度.
【答案】(1)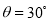 (2)
(2)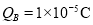 (3)
(3)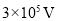 (4)
(4)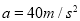
(1)渐近线II表示B的重力势能随位置的关系关系,
即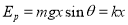
则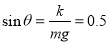
即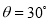
(2)由图乙中的曲线I可知,在x=6m处总势能最小,动能最大,该位置B受力平衡,则有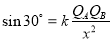
即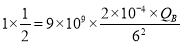 ,解得
,解得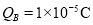
(3)M点的电势能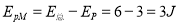
M点的电势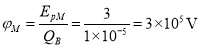
(4)在M点B球总势能为6J,根据能量守恒定律,当B的动能为零,总势能为10J,
由曲线I知B离A最近距离为x=2m
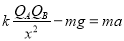
解得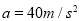
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
