某厂拟用集装箱托运甲、乙两种货物,集装箱的体积、重量、可获利润和托运能力等限制数据列在表中,如何设计甲、乙两种货物应各托运的箱数可以获得最大利润,最大利润是多少?
某厂拟用集装箱托运甲、乙两种货物,集装箱的体积、重量、可获利润和托运能力等限制数据列在表中,如何设计甲、乙两种货物应各托运的箱数可以获得最大利润,最大利润是多少?
货物 | 体积 | 重量 | 利润 |
甲 | 5 | 2 | 20 |
乙 | 4 | 5 | 10 |
托运限制 | 24 | 13 |
当托运甲4箱,乙1箱时利润最大,最大利润为9000元。
【解析】首先设甲、乙两种货物应各托运的箱数为x,y,由已知条件和表格中的数据得到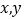 的线性约束条件,将所求的利用用
的线性约束条件,将所求的利用用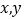 表示,将实际问题转化为线性规划求最值问题
表示,将实际问题转化为线性规划求最值问题
设甲、乙两种货物应各托运的箱数为x,y,则
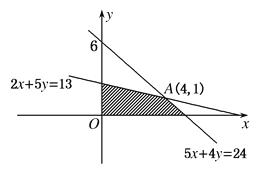
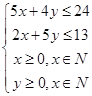
目标函数z=20x+10y,画出可行域如图.
由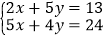 得A(4,1).
得A(4,1).
易知当直线2x+y=0平移经过点A(4,1)时,z取得最大值.且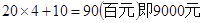
答:当托运甲4箱,乙1箱时利润最大,最大利润为9000元。
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!

 箱
箱
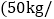 箱
箱 百元
百元 箱
箱