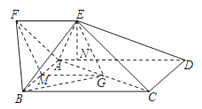
如图，四边形ABCD为矩形，四边形ADEF为梯形，AD∥FE，∠AFE=60°，且平面ABCD⊥平面ADEF，AF=FE=AB=<img alt="1" src="

如图，四边形ABCD为矩形，四边形ADEF为梯形，AD∥FE，∠AFE=60°，且平面ABCD⊥平面ADEF，AF=FE=AB=AD=2，点G为AC的中点．

（Ⅰ）求证：EG∥平面ABF；

（Ⅱ）求三棱锥B﹣AEG的体积；

（Ⅲ）试判断平面BAE与平面DCE是否垂直？若垂直，请证明；若不垂直，请说明理由

【答案】

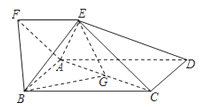
（I）证明：取AB中点M，连FM，GM．

∵G为对角线AC的中点，

∴GM∥AD，且GM=AD，

又∵FE∥AD，

∴GM∥FE且GM=FE．

∴四边形GMFE为平行四边形，即EG∥FM．

又∵EG⊄平面ABF，FM⊂平面ABF，

∴EG∥平面ABF．…（4分）

（Ⅱ）解：作EN⊥AD，垂足为N，

由平面ABCD⊥平面AFED，面ABCD∩面AFED=AD，

得EN⊥平面ABCD，即EN为三棱锥E﹣ABG的高．

∵在△AEF中，AF=FE，∠AFE=60°，

∴△AEF是正三角形．

∴∠AEF=60°，

由EF∥AD知∠EAD=60°，

∴EN=AE∙sin60°=．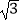

∴三棱锥B﹣AEG的体积为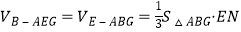=XX2X2X=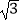

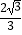
（Ⅲ）解：平面BAE⊥平面DCE．证明如下：

∵四边形ABCD为矩形，且平面ABCD⊥平面AFED，

∴CD⊥平面AFED，

∴CD⊥AE．

∵四边形AFED为梯形，FE∥AD，且∠AFE=60°，

∴∠FAD=120°．

又在△AED中，EA=2，AD=4，∠EAD=60°，

由余弦定理，得ED=2．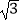

∴EA2+ED2=AD2 ，

∴ED⊥AE．

又∵ED∩CD=D，

∴AE⊥平面DCE，

又AE⊂面BAE，

∴平面BAE⊥平面DCE．

【解析】

（Ⅰ）取AB中点M，连接MG，则EF∥MG，①即得证．

（Ⅱ）转换三棱锥B﹣AEG为E﹣ABG即可求得体积．

（Ⅲ）只要证明AE⊥CDE即可．

【考点精析】关于本题考查的平面与平面垂直的性质，需要了解两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直才能得出正确答案．