如图，在三棱锥P﹣ABC中，PA⊥平面ABC，AC⊥AB，AP=BC=4，∠ABC=30°，D、E分别是BC、AP的中点，

如图，在三棱锥P﹣ABC中，PA⊥平面ABC，AC⊥AB，AP=BC=4，∠ABC=30°，D、E分别是BC、AP的中点，

（1）求三棱锥P﹣ABC的体积；

（2）若异面直线AB与ED所成角的大小为θ，求tanθ的值．

【答案】

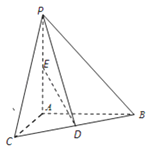
解：（1）三棱锥P﹣ABC中，

∵PA⊥平面ABC，AC⊥AB，AP=BC=4，∠ABC=30°，D、E分别是BC、AP的中点，

∴AC=2，AB=2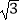，…（2分）

所以，体积VP﹣ABC=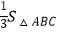•PA=．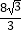

（2）取AC中点F，连接DF，EF，则AB∥DF，

所以∠EDF就是异面直线AB与ED所成的角θ．

由已知，AC=EA=AD=2，AB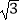=2，PC=2，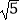

∵AB⊥EF，∴DF⊥EF．…（10分）

在Rt△EFD中，D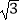F=，EF=，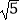

所以，tanθ=．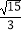

【解析】

（1）三棱锥P﹣ABC中，由PA⊥平面ABC，AC⊥AB，AP=BC=4，∠ABC=30°，D、E分别是BC、AP的中点，知AC=2，AB=2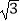 ， 由此能求出三棱锥P﹣ABC的体积．

（2）取AC中点F，连接DF，EF，则AB∥DF，所以∠EDF就是异面直线AB与ED所成的角θ，由此能求出tanθ．

【考点精析】利用异面直线及其所成的角对题目进行判断即可得到答案，需要熟知异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系．