已知等差数列{an}中，a1=12，公差为d，a3＞0，当且仅当n=3时|an|最小．

已知等差数列{an}中，a1=12，公差为d，a3＞0，当且仅当n=3时|an|最小．

（Ⅰ）求公差d的取值范围；

（Ⅱ）若d∈Z（Z为整数集），求数列{|an|}的前n项和Sn的表达式．

【答案】

解：（Ⅰ）∵a3＞0，当且仅当n=3时，|an|取到最小值，

∴a3＞0，且a4+a3＜0，

∵a1=12，

∴12+2d＞0，12+3d+12+2d＜0，

解得﹣6＜d＜﹣；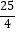

（Ⅱ）由（Ⅰ）知，d=﹣5，∴an=﹣5n+17，∴Tn=，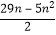

∴1≤n≤3时，Sn=，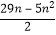

n≥4时，Sn=﹣Tn+2T3=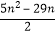+42，

∴Sn=．

【解析】

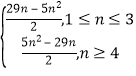（Ⅰ）根据已知条件，可得a3＞0，且a4+a3＜0，利用等差数列的通项公式列出不等式组，求出d的范围．

（Ⅱ）由（Ⅰ）知，d=﹣5，可得an=﹣5n+17，Tn=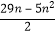 ， 分类讨论，即可求数列{|an|}的前n项和Sn的表达式．

【考点精析】根据题目的已知条件，利用等差数列的性质的相关知识可以得到问题的答案，需要掌握在等差数列{an}中，从第2项起，每一项是它相邻二项的等差中项；相隔等距离的项组成的数列是等差数列．