设m个正数a1 ， a2 ， …，am（m≥4，m∈N*）依次围成一个圆圈．其中a1 ， a2 ， a3 ， …，ak﹣1 ， ak（k＜m，k∈N*）是公差为d的等差数列，而a1 ， am ， am

设m个正数a1 ， a2 ， …，am（m≥4，m∈N*）依次围成一个圆圈．其中a1 ， a2 ， a3 ， …，ak﹣1 ， ak（k＜m，k∈N*）是公差为d的等差数列，而a1 ， am ， am﹣1 ， …，ak+1 ， ak是公比为q的等比数列．

（1）若a1=d=1，q=2，k=8，求数列a1 ， a2 ， …，am的所有项的和Sm；

（2）若a1=d=q=3，m＜2015，求m的最大值；

（3）当q=2时是否存在正整数k，满足a1+a2+…+ak﹣1+ak=3（ak+1+ak+2+…+am﹣1+am）？若存在，求出k值；若不存在，请说明理由．

【答案】

解：（1）由题意可得：ak=8，因此数列a1 ， a2 ， …，am为1，2，3，4，5，6，7，8，4，2共10个数，此时m=10，Sm=42．

（2）∵a1 ， a2 ， a3 ， …，ak﹣1 ， ak（k＜m，k∈N*）是首项为3，公差为3的等差数列，

∴ak=3k．

而a1 ， am ， am﹣1 ， …，ak+1 ， ak是公比为q的等比数列，

∴ak=3m+2﹣k ， 因此3k=3m+2﹣k ，

∴k•3k=3m+1 ，

要使m最大，则k必须最大．

又k＜m＜2015，故k的最大值为 36 ， 可得36•3729=3m+1 ， 解得m的最大值是734．

（3）由a1 ， a2 ， a3 ， …，ak﹣1 ， ak（k＜m，k∈N*）是公差为d的等差数列，可得ak=a1+（k﹣1）d．

而a1 ， am ， am﹣1 ， …，ak+1 ， ak是公比为2的等比数列，∴ak=．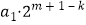

故a1+（k﹣1）d=，∴（k﹣1）d=a1（2m+1﹣k﹣1）．

又a1+a2+…+ak﹣1+ak=3（ak+1+ak+2+…+am﹣1+am），am=2a1 ，

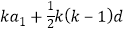∴=3×2a1×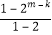，则ka1+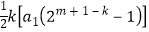=6（2m﹣k﹣1），

则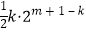+k=6（2m﹣k﹣1），即k•2m+1﹣k+k=6×2m+1﹣k﹣12，

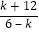k≠6，则2m+1﹣k==﹣1+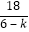，∴k＜6，

代入验证可得：当k=4时，上式等式成立，此时m=6．综上可得：当且仅当m=6时，存在k=4满足等式．

【解析】

（1）由题意可得：ak=8，因此数列a1 ， a2 ， …，am为1，2，3，4，5，6，7，8，4，2共10个数，即可得出．

（2）由于a1 ， a2 ， a3 ， …，ak﹣1 ， ak（k＜m，k∈N*）是首项为3，公差为3的等差数列，可得ak=3k．而a1 ， am ， am﹣1 ， …，ak+1 ， ak是公比为q的等比数列，可得ak=3m+2﹣k ， 因此3k=3m+2﹣k ， 要使m最大，则k必须最大．又k＜m＜2015，即可得出；

（3）由a1 ， a2 ， a3 ， …，ak﹣1 ， ak（k＜m，k∈N*）是公差为d的等差数列，可得ak=a1+（k﹣1）d．而a1 ， am ， am﹣1 ， …，ak+1 ， ak是公比为2的等比数列，可得ak=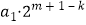 ． 故a1+（k﹣1）d= 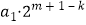， （k﹣1）d=a1（2m+1﹣k﹣1）．又a1+a2+…+ak﹣1+ak=3（ak+1+ak+2+…+am﹣1+am），am=2a1 ， 化简整理即可得出．

【考点精析】根据题目的已知条件，利用等比数列的通项公式（及其变式）和等比关系的确定的相关知识可以得到问题的答案，需要掌握通项公式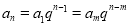：；等比数列可以通过定义法、中项法、通项公式法、前n项和法进行判断．