已知函数f（x）<img alt="1" src="/tk/20210512/1620760311164.png"/>（k＞0）

已知函数f（x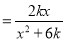）（k＞0）

（1）若f（x）＞m的解集为{x|x＜-3，或x＞-2}，求不等式5mx2+kx+3＞0的解集；

（2）若存在x＞3，使得f（x）＞1成立，求k的取值范围．

【答案】

（1）（2）

【解析】

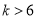
（1）根据不等式解集与对应方程根的关系：-3，-2是方程mx2-2kx+6km=0的根，即利用韦达定理得方程组，解方程组可得m,k的值，代入不等式5mx2+kx+3＞0再解一元二次不等式即可（2）不等式有解问题，一般转化为对应函数最值问题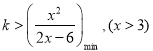： ，再根据基本不等式求最值，即得k的取值范围．

解：（1）不等式，

∵不等式mx2-2kx+6km＜0的解集为{x|x＜-3，或x＞-2}，∴-3，-2是方程mx2-2kx+6km=0的根，

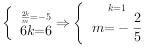∴，故有，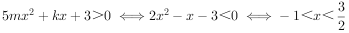

∴不等式5mx2+kx+3＞0的解集为．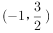

（2）．

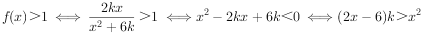存在x＞3，使得f（x）＞1成立，即存在x＞3，使得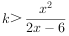成立．

令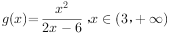，则k＞g（x）min．

令2x-6=t，则t∈（0，+∞），，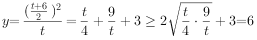

当且仅当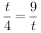即时等号成立．

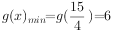∴，故k∈（6，+∞）．