已知函数<img alt="1" src="/tk/20210512/1620751955443.png"/> ， 若函数f（x）在区间[﹣2，a]

已知函数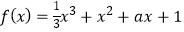 ， 若函数f（x）在区间[﹣2，a]上单调递增，则实数a的取值范围是______

【答案】

[1，+∞）

【解析】

f′（x）=x2+2x+a，

∵函数f（x）在区间[﹣2，a]上单调递增，

∴f′（x）=x2+2x+a≥0在区间[﹣2，a]上恒成立．

令g（x）=x2+2x+a，x∈[﹣2，a]．

g（x）=（x+1）2+a﹣1，

①当﹣2＜a＜﹣1时，函数g（x）在x∈[﹣2，a]单调递减，∴必有g（a）=a2+3a≥0，解得a≤﹣3或a≥0，舍去．

②当﹣1≤a时，函数g（x）在x=﹣1时取得最小值，∴必有g（x）≥g（﹣1）=1﹣2+a≥0，解得a≥1，满足条件．

综上可得：a≥1．

∴实数a的取值范围是[1，+∞）．

所以答案是：[1，+∞）．

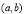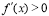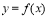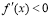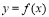【考点精析】关于本题考查的利用导数研究函数的单调性，需要了解一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减才能得出正确答案．