已知集合P＝{x|－2≤x≤10}，Q＝{x|1－m≤x≤1＋m}．
(1)求集合∁RP；
(2)若P⊆Q，求实数m的取值范围；
(3)若P∩Q＝Q，求实数m的取值范围．
【答案】(1) ∁RP＝{x|x<－2或x>10}； (2) [9，＋∞);（3）(－∞，3]．
【解析】（1）根据数轴可得结合补集（2）根据数轴可得实数m满足的条件，解不等式可得m的取值范围；（3）由P∩Q＝Q得，Q⊆P，再分空间与非空讨论，结合数轴可得实数m满足的条件，解不等式可得m的取值范围
(1)∁RP＝{x|x<－2或x>10}；
(2)由P⊆Q，需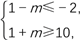
得m≥9，即实数m的取值范围为[9，＋∞);
(3)由P∩Q＝Q得，Q⊆P，
①当1－m>1＋m，即m<0时，Q＝∅，符合题意；
②当1－m≤1＋m，即m≥0时，需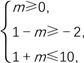
得0≤m≤3；
综上得：m≤3，即实数m的取值范围为(－∞，3]．
版权声明
声明：有的资源均来自网络转载，版权归原作者所有，如有侵犯到您的权益
请联系本站我们将配合处理！