已知椭圆C1：<img alt="1" src="/tk/20210512/1620750900249.png"/>+<img alt=&qu

已知椭圆C1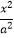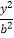：+=1（a＞b＞0）的离心率为e= 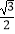， 且C1的右焦点与抛物线C2：y2=4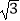x的焦点相同．

（1）求椭圆C1的方程；

（2）求经过点P（﹣2，0）分别作斜率为k1、k2（k1≠k2）的两条直线，两直线分别与椭圆C1交于M、N两点，当直线MN与y轴垂直时，求k1•k2的值．

【答案】

解：（1）∵椭圆C1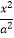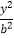：+=1（a＞b＞0）的离心率为e=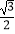，且C1的右焦点与抛物线C2：y2=4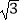x的焦点相同

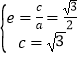∴，解得a=2，c=，

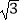b2=4﹣3=1，

∴椭圆C1的方程为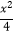+y2=1．

（2）由题意，当k1=0时，M点的纵坐标为0，直线MN与y轴垂直，则点N的纵坐标也为0，

∴k1=k2=0，与k1≠k2矛盾，∴k1≠0，

设直线PM：y=k1（x+2），

由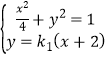，得，

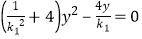解得y=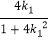或y=0（舍），

∴M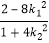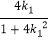（，），同理N（，），

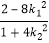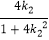∵直线MN与y轴垂直，∴=，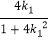

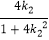化简，得，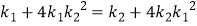

∴（k2﹣k1）（4k1k2﹣1）=0，

又由k1≠k2 ， 得4k1k2﹣1=0，

∴k1k2=．

【解析】

（1）由椭圆的离心率和且C1的右焦点与抛物线C2：y2=4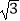x的焦点相同，列出方程组求出a，b，由此能求出椭圆C1的方程．

（2）设直线PM：y=k1（x+2），与椭圆联立，求出M，同理求出N，由直线MN与y轴垂直，得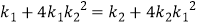 ， 由此能求出k1k2的值．