在ABC中，内角A，B，C的对边分别为a，b，c，已知<img alt="1" src="/tk/20210512/1620750879223.png"/

在ABC中，内角A，B，C的对边分别为a，b，c，已知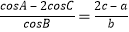

（Ⅰ）求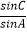的值；

（Ⅱ）若cosB= ， b=2，求△ABC的面积S．

【答案】

解：（Ⅰ）由正弦定理设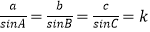

则===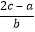

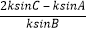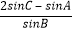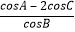
整理求得sin（A+B）=2sin（B+C）

又A+B+C=π

∴sinC=2sinA，即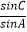=2

（Ⅱ）由余弦定理可知cosB=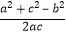=①

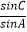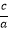由（Ⅰ）可知==2②

再由b=2，①②联立求得c=2，a=1

sinB==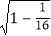

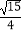
∴S=acsinB=

【解析】

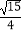
（Ⅰ）利用正弦定理把题设等式中的边转化成角的正弦，整理后可求得sinC和sinA的关系式，则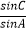的值可得．

（Ⅱ）先通过余弦定理可求得a和c的关系式，同时利用（Ⅰ）中的结论和正弦定理求得a和c的另一关系式，最后联立求得a和c，利用三角形面积公式即可求得答案．