△ABC外接圆半径为<img alt="1" src="/tk/20210512/1620751993597.png"/> , 内角A,B,C对应的
△ABC外接圆半径为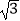 , 内角A,B,C对应的边分别为a,b,c,若A=60°,b=2,则c的值为______
, 内角A,B,C对应的边分别为a,b,c,若A=60°,b=2,则c的值为______
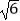 +1
+1
解: ∵△ABC外接圆半径为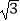 , 内角A,B,C对应的边分别为a,b,c,若A=60°,b=2,
, 内角A,B,C对应的边分别为a,b,c,若A=60°,b=2,
∴由正弦定理可得: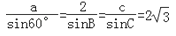 , 解得:a=3,
, 解得:a=3,
∴利用余弦定理:a2=b2+c2﹣2bccosA,可得:9=4+c2﹣2c,即c2﹣2c﹣5=0,
∴解得:c=1+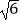 , 或1﹣
, 或1﹣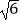 (舍去).
(舍去).
所以答案是: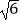 +1.
+1.
【考点精析】利用余弦定理的定义对题目进行判断即可得到答案,需要熟知余弦定理: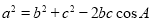 ;
;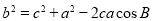 ;
;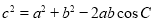 .
.
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
