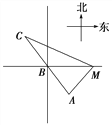
如图所示，已知A、B、C是一条直路上的三点，AB与BC各等于1 km，从三点分别遥望塔M，在A处看见塔在北偏东45°方向，在B处看塔在正东方向，在点C处看见塔在南偏东60°方向，求塔到直路ABC的最短

如图所示，已知A、B、C是一条直路上的三点，AB与BC各等于1 km，从三点分别遥望塔M，在A处看见塔在北偏东45°方向，在B处看塔在正东方向，在点C处看见塔在南偏东60°方向，求塔到直路ABC的最短距离．

【答案】

【解析】

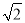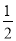由S△MAB与S△MBC底相同高相同得S△MAB＝S△MBC；利用三角形面积公式代入整理得MC＝MA，然后根据余弦定理得AC2＝MA2＋MC2－2MA·MC·cos 75°＝MA；最后根据三角形的面积公式得 MA·MC·sin 75°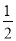＝AC·h，整理求出h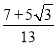＝(km).

试题解析：

由题意∠CMB＝30°，∠AMB＝45°，

因为AB＝BC＝1，所以S△MAB＝S△MBC，

即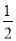MA·MB·sin 45°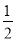＝MC·MB·sin 30°，

所以MC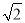＝MA，

在△MAC中，由余弦定理AC2＝MA2＋MC2－2MA·MC·cos 75°，

所以MA2＝，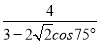

设M到AB的距离为h，则由△MAC的面积得

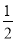MA·MC·sin 75°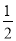＝AC·h，

所以h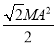＝·sin 75°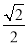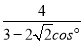＝··sin 75°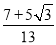＝(km)．