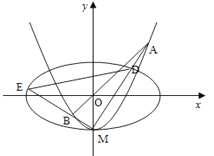
如图，椭圆C1：<img alt="1" src="/tk/20210512/1620750767432.png"/>+<img alt=&q
如图，椭圆C1：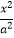
+
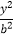=1（a＞b＞0）的离心率为
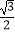， x轴被曲线C2：y=x2﹣b截得的线段长等于C1的长半轴长．求C1 ， C2的方程
解：由题得e=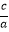
=
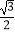，从而a=2b，又2
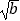=a，解得a=2，b=1，
故C1 ， C2的方程分别为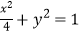
，y=x2﹣1．
先利用离心率得到一个关于参数的方程，再利用x轴被曲线C2：y=x2﹣b截得的线段长等于C1的长半轴长得另一个方程，两个方程联立即可求出参数进而求出C1 ， C2的方程.
【考点精析】掌握椭圆的标准方程是解答本题的根本，需要知道椭圆标准方程焦点在x轴：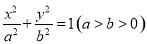
，焦点在y轴：
．
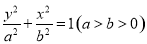版权声明
声明：有的资源均来自网络转载，版权归原作者所有，如有侵犯到您的权益
请联系本站我们将配合处理！