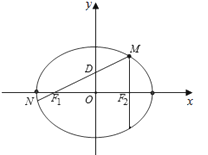
设F1 ， F2分别是C：<img alt="1" src="/tk/20210512/1620750848166.png"/>+<img a

设F1 ， F2分别是C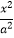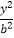：+=1（a＞b＞0）的左，右焦点，M是C上一点且MF2与x轴垂直，直线MF1与C的另一个交点为N．

（1）若直线MN的斜率为 ， 求C的离心率；

（2）若直线MN在y轴上的截距为2，且|MN|=5|F1N|，求a，b．

【答案】

解：（1）∵M是C上一点且MF2与x轴垂直，

∴M的横坐标为c，当x=c时，y=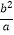，即M（c，），

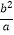若直线MN的斜率为，

即tan∠MF1F2=，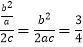

即b2=ac=a2﹣c2 ，

即c2+ac﹣a2=0，

则，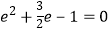

即2e2+3e﹣2=0

解得e=或e=﹣2（舍去），

即e=．

（Ⅱ）由题意，原点O是F1F2的中点，则直线MF1与y轴的交点D（0，2）是线段MF1的中点，

设M（c，y），（y＞0），

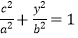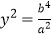则，即，解得y=，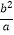

∵OD是△MF1F2的中位线，

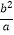∴=4，即b2=4a，

由|MN|=5|F1N|，

则|MF1|=4|F1N|，

解得|DF1|=2|F1N|，

即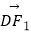=2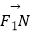

设N（x1 ， y1），由题意知y1＜0，

则（﹣c，﹣2）=2（x1+c，y1）．

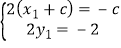即，即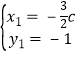

代入椭圆方程得，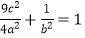

将b2=4a代入得，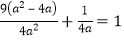

解得a=7，b=2．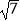

【解析】

（1）根据条件求出M的坐标，利用直线MN的斜率为 ， 建立关于a，c的方程即可求C的离心率；

（2）根据直线MN在y轴上的截距为2，以及|MN|=5|F1N|，建立方程组关系，求出N的坐标，代入椭圆方程即可得到结论．