已知各项是正数的数列<img alt="1" src="/tk/20210511/1620711891915.png"/>的前n项和为<img
已知各项是正数的数列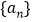 的前n项和为
的前n项和为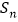 .
.
(1)若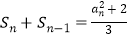 (nN*,n≥2),且
(nN*,n≥2),且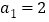 .
.
①求数列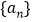 的通项公式;
的通项公式;
②若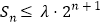 对任意
对任意 恒成立,求实数
恒成立,求实数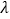 的取值范围;
的取值范围;
(2)数列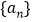 是公比为q(q>0, q1)的等比数列,且{an}的前n项积为
是公比为q(q>0, q1)的等比数列,且{an}的前n项积为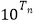 .若存在正整数k,对任意nN*,使得
.若存在正整数k,对任意nN*,使得 为定值,求首项
为定值,求首项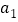 的值.
的值.
(1)①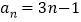 ②
②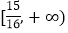 (2)
(2)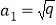
(1)①当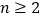 时,由
时,由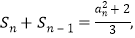 可得
可得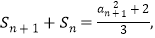 两式相减得
两式相减得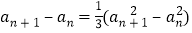 ,即
,即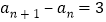 ,
,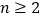 ,数列
,数列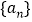 为等差数列,可得
为等差数列,可得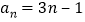 ,②由①知,
,②由①知,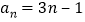 ,所以
,所以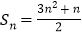 ,可得
,可得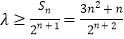 对一切
对一切 恒成立,记
恒成立,记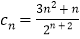 ,,判断数列
,,判断数列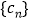 的单调性,求出最大项,从而可得结果;(2)设
的单调性,求出最大项,从而可得结果;(2)设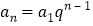 (
(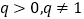 ),
),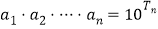 ,两边取常用对数,
,两边取常用对数,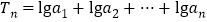 . 令
. 令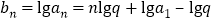 ,则数列
,则数列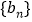 是以
是以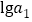 为首项,
为首项,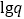 为公差的等差数列, 若
为公差的等差数列, 若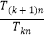 为定值,令
为定值,令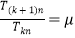 ,化为.
,化为.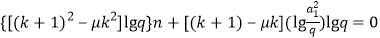 对
对 恒成立,问题等价于
恒成立,问题等价于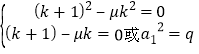 ,从而可得结果.
,从而可得结果.
(1)①当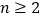 时,由
时,由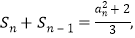
则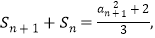
两式相减得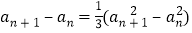 ,即
,即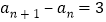 ,
,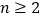
当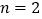 时,
时,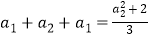 ,即
,即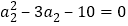 ,
,
解得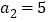 或
或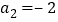 (舍),
(舍),
所以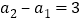 ,即数列
,即数列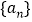 为等差数列,且首项
为等差数列,且首项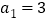 ,
,
所以数列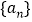 的通项公式为
的通项公式为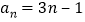 .
.
②由①知,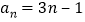 ,所以
,所以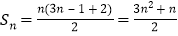 ,
,
由题意可得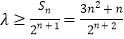 对一切
对一切 恒成立,
恒成立,
记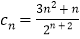 ,则
,则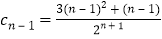 ,
,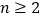 ,
,
所以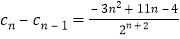 ,
,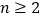 ,
,
当 时,
时,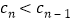 ,当
,当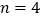 时,
时,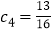 ,且
,且 ,
,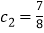 ,
,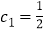 ,
,
所以当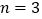 时,
时,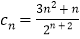 取得最大值
取得最大值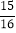 ,
,
所以实数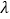 的取值范围为
的取值范围为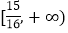 .
.
(2)由题意,设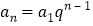 (
(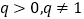 ),
),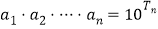 ,两边取常用对数,
,两边取常用对数,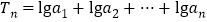 . 令
. 令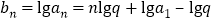 ,则数列
,则数列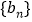 是以
是以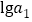 为首项,
为首项,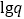 为公差的等差数列, 若
为公差的等差数列, 若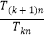 为定值,令
为定值,令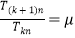 ,则
,则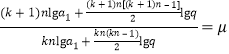 ,
,
即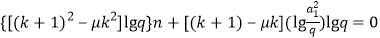 对
对 恒成立,
恒成立,
因为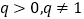 ,问题等价于
,问题等价于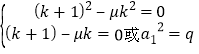
将 代入
代入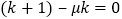 ,解得
,解得 .
.
因为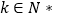 ,所以
,所以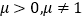 ,
,
所以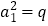 ,又
,又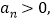 故
故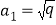 .
.
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
