设函数f(x)=|x﹣a|+3x,其中a>0
(Ⅰ)当a=1时,求不等式f(x)≥3x+2的解集;
(Ⅱ)若不等式f(x)≤0的解集为{x|x≤﹣3},求a的值.
【答案】解:(Ⅰ)当a=1时,f(x)≥3x+2可化为
|x﹣1|≥2.
由此可得x≥3或x≤﹣1.
故不等式f(x)≥3x+2的解集为:
{x|x≥3或x≤﹣1}.
(Ⅱ)由f(x)≤0得:
|x﹣a|+3x≤0,
此不等式化为不等式组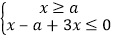 或
或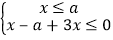 ,
,
即 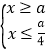 或
或 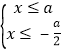 ,
,
因为a>0,所以不等式组的解集为{x|x≤﹣ },
},
由题设可得﹣ =﹣3,故a=6.
=﹣3,故a=6.
(Ⅰ)当a=1时,f(x)≥3x+2可化为|x﹣1|≥2.直接求出不等式f(x)≥3x+2的解集即可.
(Ⅱ)由f(x)≤0得|x﹣a|+3x≤0分x≥a和x≤a推出等价不等式组,分别求解,然后求出a的值.
【考点精析】根据题目的已知条件,利用绝对值不等式的解法的相关知识可以得到问题的答案,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.
版权声明
声明:有的资源均来自网络转载,版权归原作者所有,如有侵犯到您的权益
请联系本站我们将配合处理!
