在直角坐标平面内，以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系．已知点A、B的极坐标分别为<img alt="1" src="/tk/20210512/16

在直角坐标平面内，以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系．已知点A、B的极坐标分别为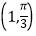、 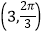， 曲线C的参数方程为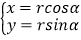(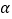为参数）．

（Ⅰ）求直线AB的直角坐标方程；

（Ⅱ）若直线AB和曲线C只有一个交点，求r的值．

【答案】

解：（Ⅰ）∵点A、B的极坐标分别为、，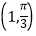

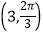∴点A、B的直角坐标分别为、，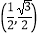

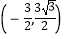∴直线AB的直角坐标方程为；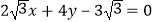

（Ⅱ）由曲线C的参数方程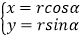(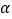为参数），化为普通方程为x2+y2=r2 ，

∵直线AB和曲线C只有一个交点，

∴半径r==．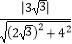

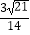【解析】

（Ⅰ）由x=ρcosθ，y=ρsinθ，可将A，B化为直角坐标，再由直线方程的形式，即可得到AB的方程；

（Ⅱ）运用同角的平方关系，可将曲线C化为普通方程即为圆，再由直线和圆相切：d=r，即可得到半径r．